NESTED GEOMETRIESAutumn 2015
Academic ARCHUD 122: Studio II Faculty: Katy Barkan & Heather Roberge UCLA School of Architecture & Design |
|
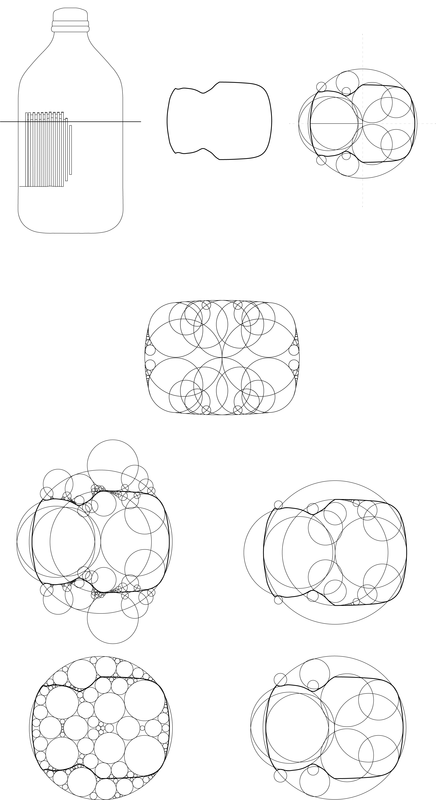
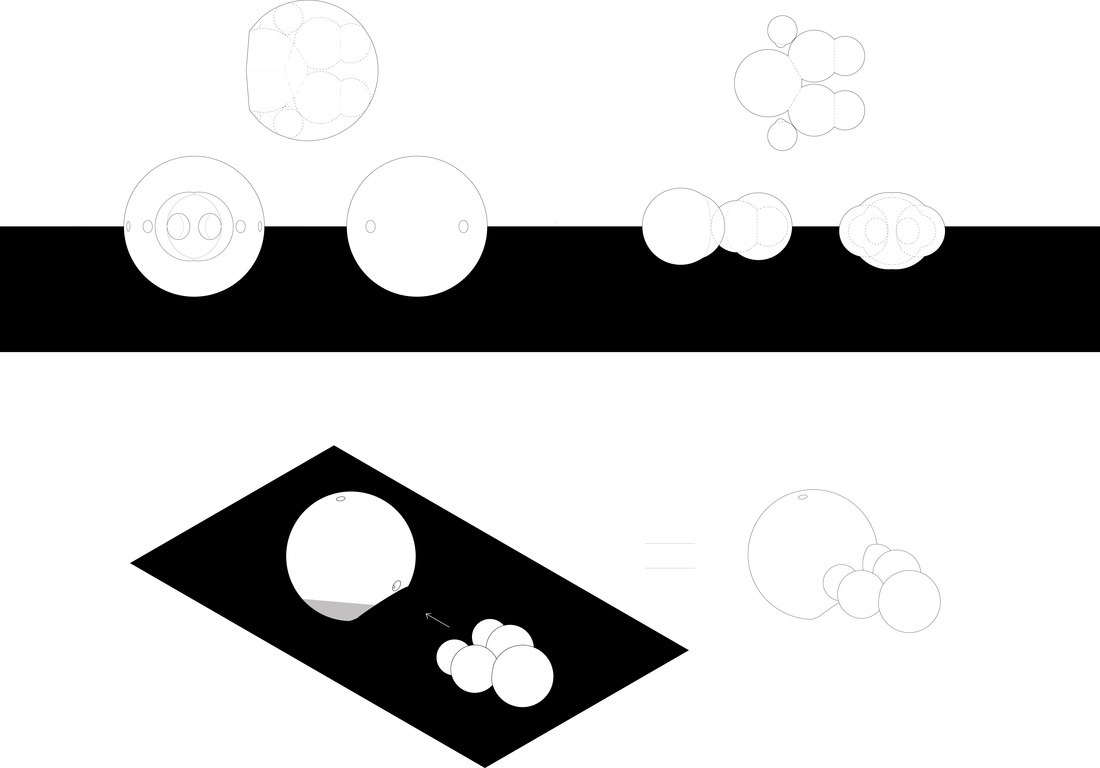
Our initial strategy presented us with the task to digitally model a milk jug, carton, or bottle. After cutting the object in a selected area, I investigated the existing geometries of the bottle. Strictly using only circles, I began to recreate the bottle using these found geometries, and explored the different sphere + sphere relationships. The project challenged notions of inside vs. outside, positive vs. negative geometries, as the distinction between the two became ambiguous at times. As one travels through the space, one alternates between inside or outside of the negative and positive elements. For example, being inside the positive elements means you’re outside the negative, and vice versa. Only at one single moment are these two different series of spheres connected (highlighted by the red below), allowing one to travel in between positive/negative spaces.
|
|
INHERENT GEOMETRIES IN EVERYDAY OBJECTS
After taking a single cut from the original milk jug form, the inherent geometries were explored. Through the use of tangents of circles, the curve of the cut was reproduced. In a way, the geometries of the milk jug were recreated via 2D circles.
|
|
Iterations of initial inherent-geometry-exploration.
|
FORMAL STRATEGY - FINAL FORMThe geometries derived from the original cut were brought into 3D, transformed into spheres. A positive and negative of the forms were created. The two were then conjoined to create a new, unified form.
|
The geometries derived from the original cut were brought into 3D, transformed into spheres. A positive and negative of the forms were created. The two were then conjoined to create a new, unified form.
INSIDE vs. OUTSIDE |
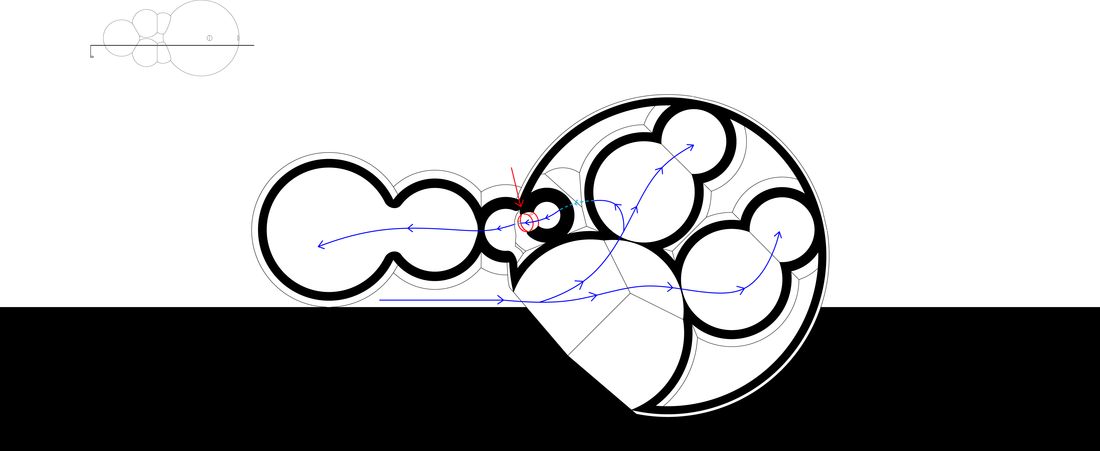
As one travels through the space, one alternates between inside or outside of the negative and positive elements. For example, being inside the positive elements means you're outside the negative, and vice versa. Only at one single moment are these two different series of spheres connected (highlights by the red markings above), allowing one to travel in between positive/negative spaces.
Serial plans
